第8章 非線形性とミクロ経済学

宮澤政権と麻生政権は適切な経済対策を行ったにもかかわらず，国民の手で引きずりおろされる結果となった。その理由のひとつに，

デフレ対策は直感とずれる

ということが挙げられる。

ミクロの経済主体である家計・企業にとって，ほとんどの場合，マクロ経済政策は異様なものに映る。それゆえ，デフレ対策を行った首相は失脚し，以下のような「直観的だが間違った考え方」が支持されてきた（全体-個別の誤謬）。

しかし，なぜ「直感とずれる」ということが生じるのだろうか。その理由は

経済現象の複雑性

に起因する。第8～9章では複雑性がどのような経路をたどってミクロとマクロの断裂を引き起こしているのか説明する。

第8～9章の内容は学問の本質にかかわる部分であり，その内容はこれまで以上に抽象的となる。そのため，学問的なバックグラウンドがなければ，ここに書かれていることは一度読んだだけでは理解できないかもしれない。

もっとも，完全に理解できなかったとしても，それ以降の内容を理解するうえで大きな障害になるわけではない。読み飛ばしたい人は，第9章の4だけなぞれば十分と思われる。

• マクロ経済学的アプローチ
  マクロ経済学の意義について（第9章 - 4）

1．複雑系としての経済現象

経済とは個々の経済活動（商取引など）の集積である。しかし，そこにいる人々が誰ひとり不況にしたくないと思っていても不況になることはあるし，誰ひとりハイパーインフレにしたくないと思っていてもハイパーインフレになることはある。すなわち，マクロ経済はミクロの単純な集積によって説明することができない。

このような特徴は複雑性と呼ばれ，その性質を持つシステムは複雑系と呼ばれる。結論からいえば，

• マクロ経済政策が個人（ミクロ）の直感と乖離すること
• 300年後の日食日時は正確に予測できるのに，翌日の株価は正確に予測できないこと
• 計画経済がうまく機能しないこと

は，いずれも究極的には複雑性を持つ構造が理由である。

なお，後述するように，「複雑」の定義は学者によって若干異なるが，マクロ経済はほとんどすべての定義において複雑に該当する。したがって，以下のような主張は「定義上」間違いといっていい。

① 経済現象と経済学の関係

経済が複雑であるのに対し，それを表現する手段は限られている。したがって，経済現象と経済学の間にはギャップが存在する。以下の3つの主張はそのことを誤解している例だ。

A：経済現象と経済学の混同

経済学のモデルが単純だったからといって，実際の経済現象が単純なわけではない。第2章において「基礎的な」経済学と強調した理由もここにある。単純なモデルは現実の限定的な近似でしかなく，それをもって経済全体を理解した気になるのは危険である。

• 「基礎的な」経済学の理論
  現実離れした前提の存在（第2章）

B：誤った経済学楽観論

確かに，単純な経済モデルを引っ張ってきて，鬼の首を取ったかのように批判している者は多い。その手の批判はモデルを改良すれば事足りるため，既に経済学者によって解決されている場合が大半であり，上記のツイートには一定の正当性がある。

しかし，モデル改良による精度の向上には限界がある。このことは多くの人が認めるだろうが，より重要な点は，

社会科学において，モデル改良の限界はかなり早い段階で訪れる

ということだ。実際，上記のような主張をする者は，経済学を物理学などの自然科学と同列に扱っていることが多い。このことは第9章で説明する。

C：誤った経済学悲観論

モデル改良に限界があることを考慮すれば，経済学が経済現象を十分に表現できていないことは事実といっていい。しかし，上記の主張は，

• 経済学が経済現象を十分に表せていないこと
• 経済学が役に立たないこと

を混同している。

仮に何らかの理論が特定の部分でしか機能しなかったとしても，その「特定の部分」で役に立つことは間違いない。つまり，「基礎的な」経済学の単純なモデルであっても，それが有効に機能する場合はあるし，「単純だから役に立たたない」という結論にはならない。役に立たないように見えるのはその適用方法を理解していないためである。

これも第9章で述べるが，「誤った悲観論」は「誤った楽観論」と同様，社会科学に対する誤解が根底にある。上記の楽観論と悲観論は

現在のあらゆるデータから，将来の不況や資産価格を予想するシステムを作ることは可能か

という質問に対して肯定的か否定的かという違いしかない。

予測システムを構築することやモデルの精度向上を目指すことには価値がある。しかし，経済現象の場合，自然科学ではあまりみられない重要な問題があり（第9章で説明），早い段階で限界が訪れる。それえゆえ，社会科学固有のアプローチが必要になるが，「誤った楽観論」と「誤った悲観論」はどちらもその認識が欠けている。

• 巨大予測システムの陥穽
  なぜ経済予測はうまくいかないのか（第9章 - 3）

② 複雑系の特徴

第8～9章にかけて，複雑系におけるいくつかの特徴と経済学（社会科学）の関係について説明する。具体的には次の3つを取り上げる。

• 特徴1：非線形性（第8章）
• 特徴2：創発（第9章）
• 特徴3：自己組織化（第9章）

• ※ このサイトにおいて，上記の特徴は「複雑性の段階」と捉えてもらってもかまわない。

本来なら複雑性の定義から始めるべきかもしれないが，前述の通り，複雑性の定義は人によって異なる[1]。また，それについて詳述することは当サイトの趣旨からも外れてしまう。そこで，ここでは定義ではなく「特徴」を取り上げ，それと経済学がどのように対応しているのかを中心に説明する。

2．非線形性

なぜマクロの現象をミクロの単純な合計で表せない場合があるのだろか。その理由のひとつは非線形性が存在するためだ。これは複雑性における第1段階の特徴といえる。

非線形性

全体が個別の1次関数で表現できないような関係。

たとえば，学校の試験（国数英3科目）で，

• 国語で過去最高得点
• 数学で過去最高得点
• 英語で過去最高得点

となれば，その総和である全体の点数も過去最高得点になる（線形性）。その構造は各科目の配点がどのようになっても変わらないし，「数学の点数が上がったために全体の点数が下がった」というようなことも起こらない。

しかし，関係が非線形の場合はそうならない。たとえば，ファッションにおいて，

• 自分が一番気に入っているインナー（シャツ）
• 自分が一番気に入っているアウター（上着）
• 自分が一番気に入っているパンツ（ズボン）

を組み合わせたからといって，それが最高のファッションになるとは限らない（非線形性）。シャツや上着といった個別の要素のみならず，要素間の関係性も全体のコーディネートに影響するためだ。

したがって，非線形の場合，

個々の部品・素材が良くても，その組み合わせが悪い

という可能性が存在する。組合せに問題の原因があるならば，全体（マクロ）を個別の部品（ミクロ）に分解して検証しても解決することはない。これこそが全体-個別の誤謬を生み出している主要因である。

なお，第4部 Part 1で説明するが，人間関係は非線形性の最たる例である。個別最適の合計が全体最適と一致しない例は野球などのチームスポーツや企業の人事マネジメントなどで頻繁にみられる。優れた個人がそろっているからといって，チームとして優れているとは限らない。仮に人間関係が線形性を満たすならば，経営組織論は1行で完結するだろう。

ポートフォリオ理論

直感に反する非線形性の例としてポートフォリオ理論を取り上げる。この例は人間関係などと比べれば非常に単純であり，それゆえ比較的容易に数値で表すことができる。

たとえば，以下のような期待リターンとリスクの株があったとする。

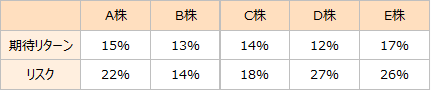
• ※ 期待リターンは将来のリターンの期待値，リスクは将来のリターンの標準偏差で定義している。

このときD株は最も期待リターンが低いにもかかわらず，最もリスクが高い。一見すると，このような株を購入することは合理的ではないように思われる。

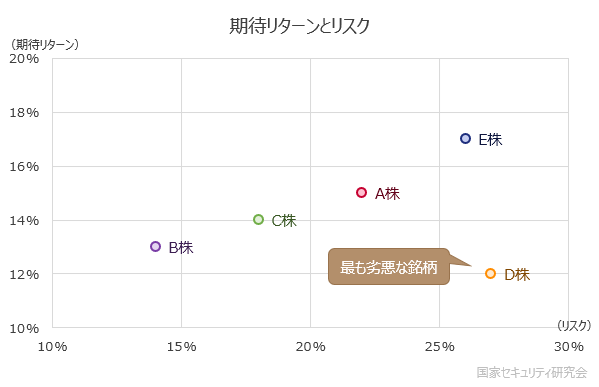
しかし，これらの株に以下のような相関関係があったとする。

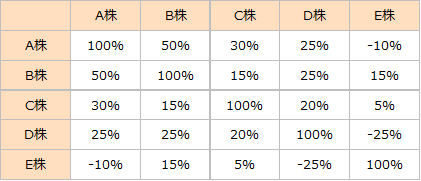
• ※ 相関係数は直線的な関係の強さを表している。プラスのとき順相関，マイナスのとき逆相関，ゼロのとき無相関。

このとき，以下の比率で株を組合せれば，A～D株よりも期待リターンが高い状態で最もリスクの低いポートフォリオを組成できる。

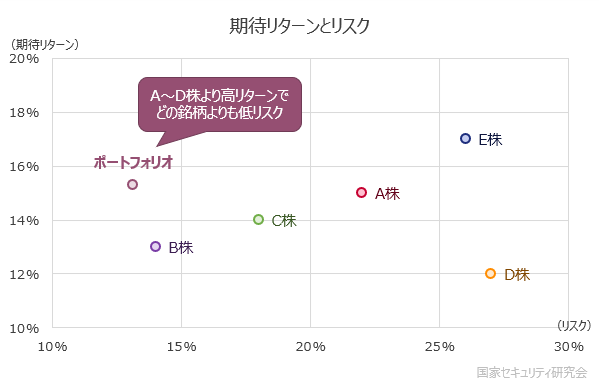
• ※ ポートフォリオの計算は別ページに記載。

ここで注目すべきは，役に立たないと思われていたD株が7.0%も組み入れられていることである。これはほとんどの人の直観に反するだろう。ミクロの視点に基づく判断が問題なのは，D株のような存在が排除されてしまうことにある。

これと同様の問題はバブル期の銀行経営についても指摘されている[2]。簡略化していえば，次のような仮説だ。当時の銀行は低リスク・高リターンの案件を優先して融資を行ってきた。一見当たり前のようだが，バブル期において低リスク・高リターンの案件はほとんど不動産業に集中していたため，バブル崩壊に伴う地価下落で一斉に不良債権化することとなった。この仮説は，個別にリスクが低かったとしても，全体でみれば思わぬところにリスクが堆積している場合があるということを示している。

3．ミクロ経済学的アプローチ

以上より，要素間に何らかの関係性が存在する場合，直感とずれる結果がもたらされることは珍しくない。

個別の要素以外にもその関係性を考慮しなければ全体はわからないということか！つまり，マクロ経済学とは要素＋関係性の学問ということだな！

こう考えた人もいるかもしれないが，この考え方はマクロ経済学ではなくミクロ経済学である。一部で誤解されているが，ミクロ経済学とは関係性を無視して個別最適を目指す学問ではない。事実，前述のポートフォリオ理論もミクロ経済学の一分野である。

それどころか，「個別最適が集まると，全体としてどのような振る舞いをするか」ということはミクロ経済学の中心的な研究分野といっていい（市場均衡分析）。

• ミクロ経済学：個々の経済活動に焦点を当てる
• マクロ経済学：経済全体の動きに注目する

市場均衡分析はミクロ経済学の中核だが，その本質は

個人とその関係を前提としてセットし，そこから市場全体がどうなるかを検証する

という個→全の流れにある。したがって，

• 特徴1：非線形性

についてはミクロ経済学のなかでも想定されており，マクロ経済学特有のものではない。ただし，このようなミクロ経済学的アプローチには大きな壁が存在する。

① 計算複雑性の問題

ミクロ経済学的アプローチにおける最大の問題は計算が複雑になるということだ。

A：解析的に解けない場合

第1に，最適化の計算はそれ自体が難しい。たとえば，前述のポートフォリオ最適化の例では簡単な関係（正規分布の相関性だけ）しか規定されていないが，その計算には確率統計，微分積分，行列ベクトルの知識が必要になる。よく経済学に対して，

人間をめちゃくちゃ単純化したモデルが採用されている！

という批判がなされるが，これ以上に複雑な関係を持ち込んだ場合，解析的に答えを出すことはほぼ不可能になる。なお，物理学の多体問題にみられるよう，こうしたケースは数学において珍しいわけではない。

多体問題

互いに相互作用する3体以上からなる系を扱う問題。二体問題までは厳密に解くことができるが，三体問題以上になると難易度は急激に上がり，解析的に解くことはできないとされている。

もっとも，多体問題がそうであるように，解析的に解くことができなくても，コンピュータシミュレーションなどによって計算することは可能である。ただし，社会現象の場合，ここで計算された答えが意味を持つとは限らない。この問題については第9章で詳述する。

• 巨大予測システムの陥穽
  コンピュータシミュレーションの限界（第9章 - 3）

B：計算負荷が大きい場合

第2に，条件を追加した最適化の計算は負荷が大きくなる。この問題は人工知能の分野などで盛んに議論されている一方，世間ではあまり認識されていない。

前述の通り，数式が解けなかったとしても，コンピュータによって計算できることはある。そうなると，

計算が難しいってだけの話でしょ？研究が進めばそういう問題は解決されるんじゃないの？

と思う人は多いだろう。しかし，計算負荷の問題は一般に思われているよりも深刻だ。

たとえば，「20個の商品をどのような組み合わせで選択することが合理的か」という問題を考える（これは前述のポートフォリオ理論とまったく同じ構造である）。これに対し，単純に組合せを比較するプログラムをコンピュータで作成し，その計算に1秒かかったとする。この場合，商品が60個に増えれば，計算には3.48万年かかることになる[3]。

商品が80個になった場合，計算時間は365億年になる。宇宙の始まり（ビッグバン）が138億年前であることを考えれば，この問題はコンピュータ性能の向上だけでどうにかなる問題ではないとわかるだろう。このように，計算の世界においては「理論上可能だが，実質的に不可能（NP困難）」という状況が存在する。

② 市場前提の非現実化

上記のような計算複雑性の問題は市場均衡を考えた場合，より致命的になる。ミクロ経済学において，市場は合理的な個人が交換を行うことで成立する。しかし，合理的な決定を行うために上記で示した複雑な計算を必要とするならば，

果たして人は消費や投資のたびにいちいちそんな難しい計算をしているのか

という疑念が浮上する。つまり，個別要素とその関係を考慮して合理的に判断するほど，その集積として表される市場は現実離れしていく。このため，完全合理性を前提とした場合，経済を十分に表現することができない。

• ※ もちろん，「全員がこう判断する場合，全体はどのようになるのか」を調べることに意味がないわけではない。しかし，それを市場の前提として組み込むのは不適切である。

この問題に対して，おそらく最初に思いつくであろう対策は

じゃあ「たまには間違える」って形にして，完全合理性の仮定を緩めればいいんじゃないの？

というものだろう。確かに「8割くらいの確率で合理的な判断をする」とすれば，少し現実に近づくようにも思われる。しかし，この方法は対策になっていない。

第1に，「たまに間違える」という形で仮定を緩めても，大半の結果は「絶対に間違えない」と仮定した場合とほとんど変わらない。もちろん，まったく同じ答えになるわけではないが，ほとんどの場合は誤差程度の違いしか表れない[4]。

第2に，複雑性の根本的な問題が反映されていない。たとえば，「100万円と10万円ならどちらを選ぶか」と聞かれれば，ほぼすべての人が100万円を選ぶだろう。簡単な選択の場合，完全合理性の前提はほとんど問題にならない。

逆にいえば，完全合理性の前提が問題となるのは複雑で難しい意思決定の場合である。特に集団心理などで「大勢の非合理的行動」は頻繁にみられるが，こうしたケースは合理的判断を確率的なものに変えても説明することはできない。これらは「たまにある計算ミス」と考えるのではなく，

複雑な状況の前では，意思決定のメカニズムが変化している

と考えるべきだろう。

• 創発と自己組織化
  自己組織化は確率的合理性で表現できない（第9章 - 1）

実際，個人が多数の商品から最適な組み合わせを考える場合，その判断がコンピュータよりも早いことは明らかだ（上で述べた通り，コンピュータによる最適化計算は商品が増えると時間がかかる）。すなわち，商品が多い場合，個人はミクロ経済学で想定されているような計算をしておらず，簡略化された手法によって意思決定を行っていることになる[5]。

③ ミクロ経済学の意義

こうした完全合理性の前提から，ミクロ経済学に対しては常に以下のような批判がなされてきた。

実際，ミクロ経済学者である松井彰彦教授（東京大学）も次のように説明している。

それに対し，われわれが提唱する手法は現実を大幅に単純化した「おもちゃ」を作り，それをもとにあれこれと仮定法を用いた議論をする。現実には存在していない制度や現象も分析対象とするため，細部にこだわっても意味がない。また登場人物はしばしば個性のないロボットとなる。

―― 松井彰彦『慣習と規範の経済学：ゲーム理論からのメッセージ』

なんだ，じゃあ結局ミクロ経済学なんて意味ないってことじゃん！

しかし，逆にいえば，「仮定を変更した場合にどう動くか」という仮説検証はミクロ経済学においてしか分析することができない。現実の描写力に劣るミクロ経済学の意義について，松井教授は次のように述べている。

しかし，われわれは別の事実を記述している。すなわち，実際にとられた行動パターンだけでなく，とることが可能であったが，実際にはとられなかった行動パターンをも記述しているのである。そのとき，われわれはとられた行動パターンととられなかった行動パターンを同列に記述する。

―― 松井彰彦『慣習と規範の経済学：ゲーム理論からのメッセージ』

経済学者J.ロビンソンが「縮尺1分の1の地図は役に立たない」と述べているように，すべてを正確に説明する理論に意味はない。重要なのは，

現実をある側面から見たとき，どのような特徴を取り出せるか

ということである。

経済学のモデルは，医者や建築家が用いる物理モデルと大差ない。病院で見かけるプラスチック製の肺のモデルは，人体のほかの部分から切り離された呼吸システムに焦点を当てている。（中略）経済学者のモデルも同じだが，物理的な構築物ではなく，言葉と数式を用いる点で異なっている。

―― D.ロドリック『エコノミクス・ルール』

このように考えた場合，「現実離れした仮定」「単純化した仮定」による経済学全体への批判は的外れと言わざるを得ない。

単純化した仮定を置いているのは単純化しても問題ないと判断されているからにすぎない。たとえば，

• 事例1：自動車販売に課税した場合，自動車の税込販売価格はどうなるか

という問題を考えるとき，多くの人々は「税込販売価格は高くなる可能性が高い」と予想できるだろう。少なくとも，税込販売価格が下落すると予想する人はいないはずだ。

重要なのは，この結論が多くの点において仮定の影響を受けないことである。上記の問題は「自動車市場が競争的かどうか」ということはあまり関係ない。また，完全合理性を仮定した場合も，その仮定を緩めた場合も，結論は変化しない。

しかし，

• 事例2：自動車の販売価格を政府が統制したら，供給量はどうなるか

という問題を考えるとき，「自動車市場が競争的かどうか」ということは決定的に重要となる。なぜなら，ミクロ経済学において，価格統制は市場が競争的ならば供給量を減少させるが，市場が独占的ならば供給量を増加させるからだ。

市場構造の仮定における重要性は事例1と事例2でまったく異なる。つまり，仮定の単純さに対する批判はそれが異なる結論につながる場合においてのみ有効となる。

経済モデルが非現実的な仮定を用いていると批判することは，ガリレオの行った斜面を転がる球体の実験で，可能な限り摩擦が生じないよう磨かれた平面が用いられていたことを批判するようなものである。

―― N.カートライト『原因の探し方，その使い方：哲学と経済学におけるアプローチ』

したがって，仮定の単純化それ自身に問題があるわけではない。問題の本質は「単純化してはいけない仮定を単純化すること」であり，それは上で述べた通り，理論の欠陥ではなく，理論の適用方法を誤っているだけである。

4．厚生経済学の第1定理

最後に市場均衡理論の解釈問題について説明する。市場均衡理論に対しては，「ミクロ経済学は非線形性を仮定していない」という誤解のもと，以下のような指摘がなされる場合がある。

よく勘違いされているが，経済学において自由競争が望ましいとされるのは，

• 競争すると切磋琢磨するから
• 競争しないとみんな怠けるから

という理由によるものではない。完全競争均衡とは

• 個人が最適化を実現しようとすれば，あたかもチームで示し合わせているかのように効率的な配分が達成される

という特殊な全体最適（見えざる手）のことであって，個別の合計が全体になる（線形性を満たしている）と想定しているわけではない。この結論は厚生経済学の第1定理という形で定式化されている。

厚生経済学の第1定理

完全競争市場においてパレート最適（誰かの効用を犠牲にせずして他の人の効用を高めることがこれ以上できない状態）が達成されるとする定理。1950年代にK.J.アローとG.ドブリューによって厳密な数学的証明が与えられた。

① 定理の解釈論争

厚生経済学の第1定理によって，2つのことが厳密に示されることとなった。ひとつは，

• 自由競争が望ましい

という結論（見えざる手）である。

もうひとつは，この定理が成立するために，

• 無数の個人と企業が存在し，すべて価格受容者として行動する
• 個人や企業の意思決定は他の消費量や生産量に左右されない
• 個人と企業は価格や効用の情報を正確に把握し，合理的に行動する
• 市場に対して参入や退出が自由

など様々な条件が必要になることである。

厚生経済学の第1定理は数学的な関係しか示していない。しかし，示された内容のどちらに重きを置くかで，その論調は180度変わる。

経済は自由競争ほど望ましい。事実，そのことは厚生経済学の第1定理で証明されている。

自由競争が望ましいという結論になるためには非常に多くの前提が必要になる。事実，そのことは厚生経済学の第1定理で証明されている。

つまり，この手の論争は価値観が必ず反映されており，多分に政治的である。

• ※ 当サイトは自由競争に懐疑的な姿勢をとっているが，その理由は日本において上記の「前提」が軽視され，自由競争重視の方に傾いてきたと解釈しているためである。この経緯についてはPart 3で詳述する。

この点にもミクロ経済学の重要な意義を見出すことができる。厚生経済学の第1定理によって前提が示されたことで，

• 市場競争に懐疑的な意見において，どの前提が満たされていないと考えているのか
• 市場競争が望ましい状態になるには，何が必要になるのか
• 自分と相手で意見が異なる場合，どの前提に対する解釈が違っているのか

といったことを整理して議論することができるようになったことだ。なお，これは上で述べた「理論の適用方法が適切か」という問題と本質的に同じである。

② 厚生と公正

理論の適用方法が適切かということを考えた場合，ミクロ経済学において最も注意を払わなければならないことは

ミクロ経済学の厚生と社会的公正は異なる

ということである。ミクロ経済学の「厚生」とはニュアンス的に「どれだけ効率的か」という概念に近い。

厚生経済学の第1定理において，完全競争市場によって達成されるパレート最適という概念は「誰かの効用を上げるには，他の誰かの効用を下げなければならない」という状況のことだ。これは世間で認識されている公正性の概念とかなり異なる。

たとえば，おにぎりだけ持っている人とハンバーガーだけ持っている人がいたとする。

両者ともどちらかだけでは飽きると思っている場合，それぞれ半分ずつ交換することによって（誰の効用も犠牲にすることなく）自らの効用水準を上げることができるだろう。

個人の選好度が異なる場合，交換はさらに進む（ミクロ経済学ではこの交換比率を価格と呼ぶ）。両者とも交換で効用が上昇しなくなったときパレート最適となる。

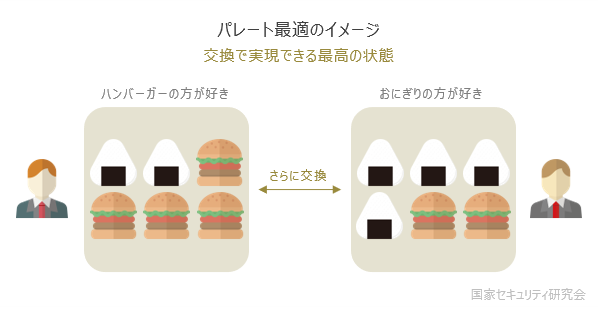
こう考えると，交換（市場経済）によって達成されるパレート最適は望ましい。ただし，注意しなければならないのは，以下のような場合もパレート最適に該当することだ。

この場合，交換によって「両者の」効用水準が上昇することはない。これが社会的に公正な状態かどうかは状況次第で意見が分かれるだろう。経済的厚生と社会的公正は必ずしも一致しない。特に社会的公正は人によって多種多様であるため，数学的に導出されることはない。この問題は第4部 Part 1で詳しく説明する。

• ^1経済学者のK.E.ボールディング教授（コロラド大学）は複雑系に関する国連大学のシンポジウム（1984年5月，モンペリエ）の第1論文において「複雑性は非常に複雑な概念である」と述べている。なお，論文では複雑性の計測手段が確立されることは今度もないであろうと予測している。
• ^2これに関連した分析レポートが日本銀行から出されている（高橋秀夫・森平爽一郎『信用リスク管理の展望 - 市場リスクとの統合されたポートフォリオアプローチ -』）。
• ^3この計算では最適化の部分プログラムが2のn乗（nは商品数）で計算されることを想定している。現在では一部の計算を簡略化することなどで負荷を軽減するシステムが開発されているが，それはあくまで「簡略化」であり，根本的な問題が解決したわけではない。
• ^4確率的な要素が含まれることによって市場の均衡が大きく異なるようなケースも存在する。これについてはPart 3で扱う。
• ^5こうした意思決定の手法は完全合理性に対して限定合理性と呼ばれている。